The Algorithms Specialization is a collection of state of the art solutions to computationally intensive tasks, as well as a guide to various problem solving paradigms in cumputer science, such as for example: divide and conquer, randomized algorithms, greedy algorithms, or dynamic programming.

Typically, algorithm performance is evaluated using the so called big Oh notation $\mathcal{O}(f(n))$, where $f(n)$ is some function of the input size ($n$ elements) roughly counting how the number of computation steps grows with input size. Ideal performance is linear $\mathcal{O}(n)$, meaning that the respective task can be performed essentially in the same amount of steps as is required to just read all of the input elements. (Colloquially, this is called a for free operation.) However, oftentimes problems can be solved in several different ways. While naive algorithms might take a polynomial or even exponential number of steps to finish, cleverly designed algorithms can accomplish the same task in a substantially smaller number of steps, that scales much better as the input size increases. Algorithm design is therefore a very important task to be able to scale real world applications to global sizes in an economic and efficient manner.

As I worked on completing the algorithms specialization, I coded c++ implementations for the various algorithms discussed. They can be found on my github page. Here, I would like to leave some notes on the covered algorithms for future reference. For each algorithm I provide a link to the header and source file of my c++ implementation.

Merge Sort

Header File, Source File
Sorting algorithms that sort objects utilizing less than or greater than comparison operations can never be quicker than $\mathcal{O}(n\log n)$ running time in the number of input elements $n$. Merge sort is one example algorithm that achieves this optimal performance by employing the divide and conquer problem solving paradigm. The sorting proceeds via recursively dividing the elements into a pair of smaller, and therefore simpler, subproblems. The division continues for a logarithmic number of iterations until most trivial base cases are reached. Subsequently, solutions to all subproblems are merged again performing a linear amount of work. One drawback of Merge Sort is that convenient and fast implementations do not sort an array in place but instead require additional working memory.

Counting Inversions

Header File, Source File
Apart from sorting an array of objects, we also might be interested in finding the number of so called inversions in that array. The number of inversions is defined as the number of pairs of elements that appear out of order in the array (e.g., in $(1,3,5,2,4,6)$ pairs $(3,2)$, $(5,2)$ and $(5,4)$ are not in increasing order, which makes $3$ inversions in total). As it turns out, the Merge Sort algorithm with very minor modifications can be used to count inversions during the sorting process. This shows that the number of inversions in an array can be found in $\mathcal{O}(n\log n)$ time as well.

Quick Sort

Header File, Source File
Quick Sort is an amazing algorithm since it employs randomization to tackle the sorting problem. On every recursive iteration, quick sort randomly selects a so called pivot element within the array of objects and transports all smaller elements to the left and all larger elements to the right of it. This way the pivot element ends up in its fully sorted position, and the recursion proceeds to sort sub-arrays of strictly smaller or strictly larger elements only. Even though in the worst case scenario quick sort might end up using a quadratic number of steps, statistically the algorithm is expected to finish in $\mathcal{O}(n\log n)$ time on average. An advantage of quick sort over merge sort is that quick sort operates in place, meaning that it does not require additional memory storage to sort a given array.

Random Select

Header File, Source File
Just as the merge sort algorithm can be easily modified to count inversions, the quick sort algorithm can be conveniently altered to find the single $i^{th}$ element of an array in its correct sorted order without actually sorting all of the array elements. This algorithm involves the same random determination of a pivot element as quick sort. However, since here we are only interested in finding and returning a single element, the recursion does not split into two smaller subproblems but requires only one. This reduces the complexity compared to quick sort, so that random select in fact, statistically is expected to finish in linear time $\mathcal{O}(n)$ on average.

Karger’s Minimum Cuts

Header File, Source File
Data sets can often be represented as graphs of nodes connected by edges defined through some notion of relationship. Given such a data set we might be interested in finding the smallest number of edges that we have to cut, or remove, in order to divide the data set into two separate data sets. One way of doing this is Karger’s algorithm, which randomly selects an edge in the graph and merges the two nodes at the two ends of the edge into one, while removing any produced self-loop edges on the resulting joint node. The merging of nodes can be parametrized, e.g., by means of a disjoint-set data structure. This process repeats until only two nodes remain, and the remaining number of edges between them represents an estimate for the minimum number of edges that needs to be cut to separate the data set into two. Certainly, a single execution of this algorithm is not guaranteed to find the minimum cut. However, repeating the algorithm $\mathcal{O}(n^2\log n)$ times, the probability of not having found the minimum cut shrinks to $\frac{1}{n}$. When the number of nodes $n$ is large, the algorithm becomes reliable and runs in $\mathcal{O}(n^2 m\log n)$ time on average, where $m$ is the total number of edges in the graph. It should be noted that nowadays several improvements of Karger’s algorithm exist that further reduce the expected running time.

Kosaraju’s Strongly Connected Components

Header File, Source File
In cases when a graph contains directed edges, meaning that the respective edge allows us to travel from one node to another but not backwards, we could ask the question: which collections of nodes form groups such that every node in the group can be reached from every other node in the group by traveling along the directed edges connecting them. Such groups are called strongly connected components of the graph. For example, the following graph:

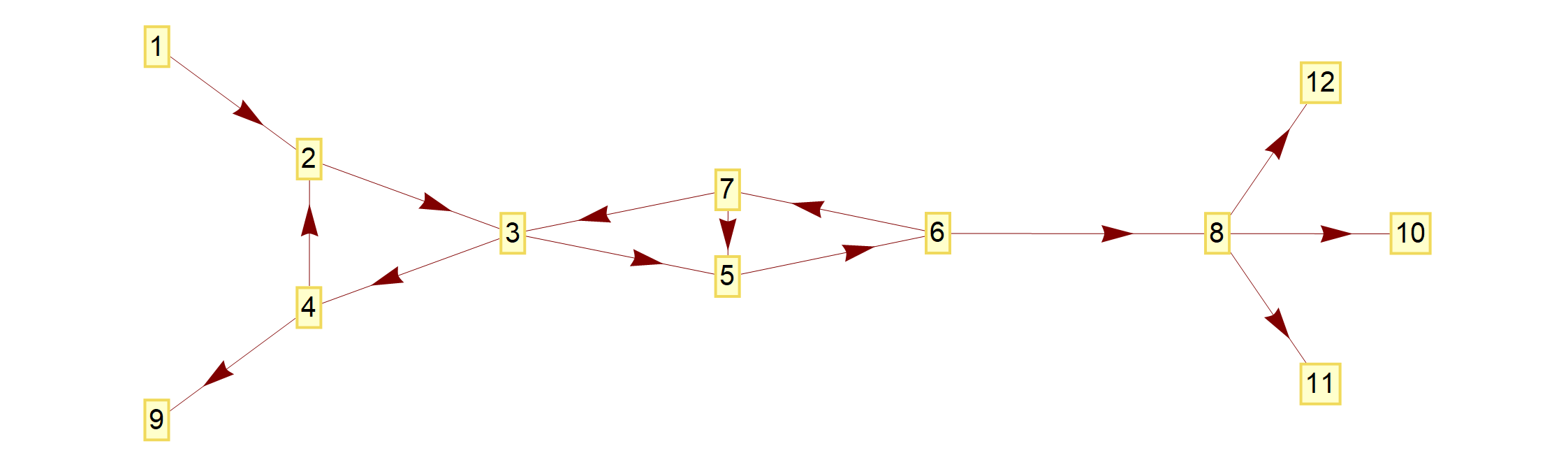
has one strongly connected component, comprised of nodes $2,3,4,5,6,7$, since each of these nodes can be reached from each other node in the strongly connected component by following edges in the specified directions.

It turns out that doing a minimal amount of book keeping, the task of finding all strongly connected components in a graph can be accomplished by essentially performing two runs of Depth-First Search (DFS) through the graph. This results in an algorithm with linear running time $\mathcal{O}(m+n)$ in the number of nodes $n$ and edges $m$ in the graph.

Dijkstra’s Shortest Paths

Header File, Source File
Some applications may involve graphs with edges that have a weight associated with them (the weight may represent a certain distance associated with traveling from one node to the other along the respective edge). In that setting we may be interested in finding a smallest overall weight path that takes us from one node to another node in the graph. In case when all edge weights are positive, Dijkstra gave a fast algorithm that constantly maintains a fronteer between already visited and not yet visited nodes in the graph. The fronteer is always extended in the direction of the cheapest edge. The cheapest edge is retrieved quickly by means of a heap data structure. This allows the algorithm to run in $\mathcal{O}(m\log n)$ time in the number of nodes $n$ and edges $m$.

Bellman-Ford Shortest Paths

Header File, Source File
Sometimes graphs contain weighted edges that can be positive as well as negative. As soon as negative edges are additionally present, Dijkstra’s Shortest Paths algorithm is not guaranteed to be correct any more. In that case we can fall back to the Bellman-Ford Shortest Paths algorithm, which starts by assigning the first node a distance zero to itself and all other nodes a distance infinity to the first node. Subsequently, during every iteration each distance is updated to the shortest possible taking neighboring nodes and their current distances into account. In a graph with $n$ nodes information takes at most $n-1$ steps to propagate from any node to any other connected node, which means the $n^{th}$ update should not produce any change in the determined distances any more. However, sometimes graphs with negative edges can contain negative weight cycles. Such a cycle can be traversed any number of times and decreases the overall weight on each traversal. This makes the question of determining shortest weight paths much more non-trivial. In such a case the current distance of each node to the first node will continue to decrease even after $n-1$ iterations. This way the Bellman-Ford algorithm conveniently allows us to determine whether a negative weight cycle exists, or to find the shortest paths weights in $\mathcal{O}(m n)$ time in the number of nodes $n$ and edges $m$.

Johnson’s All Pair Shortest Paths

Header File, Source File
Whenever we require the calculation of the shortest path not just from the first node, but from each node in a graph to all other nodes, we can run Dijkstra’s shortest paths algorithm $n$ times if all edge weights are positive. That produces a result in $\mathcal{O}(n m\log n)$ time. It would seem that to achieve the same when negative weight edges are present as well, we would have to run the Bellman-Ford shortest paths algorithm $n$ times, for a rather unsatisfactory $\mathcal{O}(n^2 m)$ running time. As it turns out, this is not the case and we can do better by using Johnson’s all pair shortest paths algorithm. It starts by adding one new node to the graph and connecting it to all other nodes in the graph by zero weight edges. Executing the Bellman-Ford algorithm on this graph once gives the shortest distances from all nodes to the newly added auxiliary node. These distances are then used to augment the weights of all incoming and outgoing edges in the original graph through addition and subtraction. It turns out that after this augmentation all edges have non-negative weights while shortest paths within the graph remain unchanged. This allows to determine the shortest paths through $n$ applications of Dijkstra’s shortest paths algorithm. Finally, edge weight augmentations are reversed through opposite subtraction and addition, which leads to an all pair shortest paths algorithm with running time $\mathcal{O}(n m\log n)$ in the number of nodes $n$ and edges $m$, regardless whether all edges have only positive weights or negative weights as well.

Prim’s Minimum Spanning Tree

Header File, Source File
Another interesting question we can ask about a graph is: what is the minimal collection of edges in the graph such that all nodes are connected and the sum of all included edge weights is minimized? Such a minimal collection of edges connecting all nodes of the graph is called a minimum spanning tree. Prim’s algorithm for computing a minimum spanning tree is similar to Dijkstra’s shortest paths algorithm. It similarly employs the heap data structure to keep track of the lowest cost edge along a frontier, and runs in $\mathcal{O}(m\log n)$ time in the number of nodes $n$ and edges $m$.

Median Maintenance

Header File, Source File
Imagine that we are receiving a continuous stream of numbers that we store in memory. At any point in time we are interested in maintaining the median value of all the numbers received so far. One way of doing this efficiently is by maintaining two heap structures containing half of the received elements each. One of the heaps keeps track of the smallest element in the upper half of the data, while the other keeps track of the largest element of the lower half. Since heap operations take $\log n$ time, this allows us to maintain a running median in $\mathcal{O}(n \log n)$ time in the number of elements $n$ received so far.

2-Sum Problem

Header File, Source File
In the 2-sum problem we are given a list of numbers and ask the question how many distinct pairs of these numbers sum up to a specified value, or a specified range of values. Since for every number in the set we are essentially interested in finding a specific matching second number, this problem can be most conveniently approached by creating a dictionary, or hash table of all available numbers. Depending on the type of hash table, finding whether a matching number is present can take logarithmic or even constant time, as opposed to linear time in a naive brute force double loop approach.

Task Scheduling

Header File, Source File
How do we optimally schedule tasks in succession that have a certain duration and completion value, such that the sum of the overall completion times of the tasks weighted by their respective completion value is minimized? This problem can be solved with a so called greedy algorithm which orders the tasks based on a single number metric such that the resulting order is optimal, without exploring multiple variations of task arrangements. We can explore scheduling the tasks in decreasing order of $value-duration$ or $\frac{value}{duration}$ criterion. It turns out that only the $\frac{value}{duration}$ criterion in decreasing order is guaranteed to produce an optimal schedule in every case.

Maximum Spacing Clustering

Header File, Source File
Given a collection of points in some space and a certain distance measure between these points, we can merge subsets of points closest to each other into clusters. As in Karger’s minimum cuts algorithm, the merging of points into clusters can be parametrized, e.g., by means of a disjoint-set data structure. Once the number of independent clusters has shrunk to a given number, we can ask what the maximized minimum distance between two points in different clusters is? Given that the clusters are accumulated by merging nodes based on a sorted list of node distances, finding the answer amounts to continuing the clustering algorithm until it encounters the next merging step.

Huffman Code

Header File, Source File
Given an alphabet of symbols, the question arises how to encode each symbol in a binary form such that an encoded message occupies an optimally least amount of memory. We assume that each symbol in the alphabet has a specific assigned weight, such as the frequency of its appearance in a typical message. Intuitively, we can afford to encode rare symbols with a larger number of bits, while frequent symbols should be encoded with a minimal number of bits. A Huffman encoding is produced by a greedy algorithm which creates a binary tree by merging pairs of rarest symbols into one and assigning the sum of their weights to the new symbol. This process continues until all symbols have been merged. Subsequently, the merging is undone in reverse order, creating the completed binary tree in the process. The greedy heuristic above guarantees that the resulting binary tree produces an optimal binary encoding of each symbol by following the path from the root node to each leaf containing the respective symbol.

Maximum Weight Independent Set

Header File, Source File
The maximum weight independent set in a path graph is a typical introductory problem to dynamic programming. A path graph of weighted nodes is essentially a list of consecutive numbers. Calculating an independent set means obtaining a subset of all nodes such that the sum of their weights is maximized, while no two neighboring nodes may be included. In dynamic programming the solution to a larger problem is obtained by finding a solution to one or more smaller sub-problems first. Different from the divide and conquer approach, the number of smaller sub-problems here is not logarithmic but rather linear in the size of the original problem. Given that only neighboring nodes may not be selected together, the relevant sub-problems in the independent set problem are the results of the same problem with one fewer node and two fewer nodes. The solution to the current problem is then the maximum of the solution to the problem with one fewer nodes or the solution of the problem with two fewer nodes plus the weight of the current last node. Naively generating the result by recursion would lead to the calculation of the same smaller sub-problems many times over. However, the use of memoization amazingly reduces the running time of the algorithm to linear $\mathcal{O}(n)$ in the number of nodes $n$.

Knapsack Problem

Header File, Source File
In the knapsack problem we are given a list of items with a specific value and weight. We have to collect a number of these items while simultaneously not exceeding an upper limit imposed on the total weight. As long as item values, weights and the knapsack capacity are reasonably sized integers, the knapsack problem is solved in polynomial time via the dynamic programming paradigm. Here we have one more parameter to keep track of compared to the maximum weight independent set problem. Therefore, the solution for the current sub-problem depends on solutions to smaller sub-problems with reduced item label as well as reduced residual capacity of the knapsack. As before, a regular table, or a hash table is used to memoize solutions to sub-problems that have already been computed, to avoid performing the same work more than once. With this the running time of this dynamic programming algorithm is $\mathcal{O}(n W)$ with number of items $n$ and knapsack capacity $W$.

Traveling Salesman

Header File, Source File
Given a number $n$ of cities and distances between all of them, what is the best route to take starting from one of the cities, visiting all cities exactly once, and returning to the initial city at the end of the trip? The best route means one with the least total distance traveled. This is a very interesting problem, as it is known to be NP-complete, which means that all known algorithms that solve this problem require a number of calculation steps that is exponential in the number of cities. Especially in this case it is therefore important to design a clever algorithm, since the scaling function will explode dramatically for large problem sizes if we are not careful. Naively, it seems that one has to consider a factorial number of permutations to find the answer, which for large number of cities $n$ would scale as $n^n$. However, as we investigate different paths, instead of the entire travel history we in fact only need to keep track of the unordered set of all cities visited so far, along with the very last city we arrived at as well as the total distance traveled so far. With this simplification the actual running time of the algorithms scales as $\mathcal{O}(n^2 2^n)$ with the number of cities $n$.

Traveling Salesman Nearest Neighbors

Header File, Source File
As discussed in the previous paragraph, for a very large number of cities $n$ the exact solution to the traveling salesman problem becomes prohibitively expensive and slow to compute. Therefore, good approximate results may be sufficient for practical intents and purposes. One approximation is given by the following greedy heuristic: in each city we scan all remaining cities that have not yet been visited and travel to the closest one, breaking ties arbitrarily. This heuristic often leads to very good approximate solutions, or in some cases to a solution that is identical to the exact solution. Since the number of cities visited is still $n$ and we scan on the order of $n$ cities to decide which one to travel to next, the running time of this approximate greedy heuristic algorithm is $\mathcal{O}(n^2)$, which is exponentially faster than finding the exact solution.

2 Satisfiability Problem

Header File, Source File
The 2 satisfiability problem is concerned with whether chains of “either, or” boolean expressions can all be satisfied simultaneously. Denoting by $!a$ the negation of $a$, such a problem might read $(a||!b)\&\&(a||c)\&\&(!b||c)$ which means (a, or not b) and (a, or c) and (not b, or c). The expression as a whole is only satisfiable if each statement in parentheses evaluates to true. One way to approach this problem is to note that each statement $(a||b)$ can be phrased in terms of two edges in a directed graph: $!a\to b$ and $!b\to a$. In this language, to be satisfiable means that no directed path through the nodes is allowed to close a loop between a boolean $a$ and its own negation $!a$. In other words, any $a$ and $!a$ are not allowed to be part of the same strongly connected component of the respective graph. By this observation, the 2 satisfiability problem essentially reduces to an application of Kosaraju’s strongly connected components algorithm mentioned above.